Cisco Networking Academy

Today I've passed the final exam for CCNA1 (Cisco Certified Network Associate). For those who don't know much about Cisco's certificates I suggest you visit this or this site. Anyway, It means I'm getting a certificate by postal mail tomorrow. I also plan to continue the Networking Academy next year with CCNA2. No.1 was all about networking theory which is pretty boring actually, but No.2 is supposed to be a lot more interesting, because it's about Cisco's devices.

New 10Mbit Line

Today I got a new Internet Line. Well, actually I should've had it 1 week ago, but there was a huge problem with the old house wiring (Our telecommunication provider - Telekom Slovenije - gave us 2 pairs of copper wires, but only one wire from each pair was used, making cancellation impossible and probably doubling the attenuation...) Anyway, we were lucky as we know somebody who works at Telekom. He came and sorted things out. Now my new VDSL line (provided by T-2) works great! Previously I had a 4/0.384 ADSL line, but now I have 10Mb/s (megabits) of download and 2Mb/s of upload speed (for about $45/month = €35.5/month)! Oh, this is not an ad! I'm just extremely happy to finally see some competition in telecommunications here in Slovenia.

4D Cube

I figured that if I had a cube that was somehow 4D (a tesseract), its diagonal (d_4) would be 2-times the length of its base side (a), and its volume would be a^4. It partly shows that dr. Michio Kaku's affirmation about formulas becoming simpler on higher dimensions is true. A tesseract to a cube is like what a cube is to a square. The thing is, that we can't really imagine something like a "4D volume", though it can be expressed mathematically (even for n-th dimension).

3D Cube:

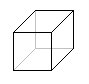
V_3 = a*a*a = a^3 (a 3D cube has 3 dimensions)
P_3 = 6*a*a = 6*a^2 (6 faces, each with a 2D surface of a^2)
d_3 = sqrt((a*sqrt(2))^2+a^2) = a*sqrt(3) (Pythagorean theorem)

4D Cube (Tesseract):

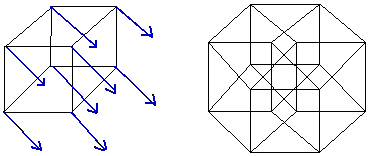
V_4 = a*a*a*a = a^4 (a 4D cube would have 4 "sides")
P_4 = 24*a^2 = 4*P_3 (count faces of a cube made from 8 cubes)
d_4 = sqrt((a*sqrt(3))^2+a^2) = 2*a (Pythagorean theorem again)

This means that a N-dimensional "cube" (the object should have its own name for each dimension) would have a diagonal: a*sqrt(N). And here is a proof that I'm not wrong.

Linux script: wa

I've created this simple and potentially useful Linux script and named it "wa"
Here it is:

#!/bin/sh
while [ $1 ]
do
clear
$1
if `test $2`
then
sleep $2
else
sleep 1
fi
done

It can be used for example for printing out different statuses, for example if you are waiting for somebody to login to the Linux box, you could use ./wa w 1
It will run a "w" command on a clean screen every second, so you don't have to constantly keep pressing w [enter] w [enter] ...
I think it's simple but convenient - the one thing Linux is missing ^^

Blog started

Blog started